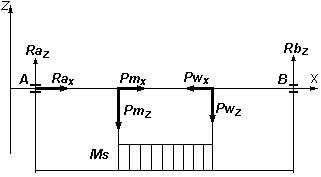
Najczęściej wał jest obciążony naprężeniami złożonymi; momentami zginającymi i momentami skręcającymi. Równanie momentów skręcających zostało wyprowadzone jako równanie momentów względem osi układu współrzędnych przebiegającej wzdłuż osi wału przy okazji obliczania sił reakcji w podporach. Aby określić moment skręcający w danym przekroju wału, należy, podobnie jak przy zginaniu podzielić wał na charakterystyczne przekroje i utworzyć równania momentów skręcających tylko dla jednej strony wału od danego przekroju. Innymi słowy przyjmujemy, że pierwszy moment względem osi wału, a więc moment powodujący jego skręcanie, z jednej strony przekroju powoduje jego skręcenie w określoną stronę, a każdy następny powoduje jego większe lub mniejsze skręcenie w zależności od kierunku działania. Czyli każdy następny jest dodawany do poprzedniego z zachowaniem kierunku działania.

Dla rozpatrywanego przykładu:

Przekrój między podporą A i kołem „m” nie jest obciążony momentem skręcającym. Przekrój między kołami „m” i „w” jest obciążony stałym momentem skręcającym równym:

Przekrój między kołem „w” i podporą B nie jest obciążony momentem skręcającym, gdyż moment z koła „m” jest równoważony momentem z koła „w”.

Wykres momentów skręcających wygląda w takim wypadku następująco:

Należy zaznaczyć, że w miejscu usytuowania kół można wyróżnić dwa momenty skręcające: zerowy i o wartości Ms. Do dalszych obliczeń wytrzymałościowych należy oczywiście zawsze wybierać moment o większej wartości bezwzględnej.

W przypadku, gdy wał jest napędzany z jednego końca oczywiście wykres i równania momentów będą odmienne. Taki przypadek omówiony jest tutaj>.

Następnym krokiem jest dobór materiału na wał.